Model skoringowy należy do grupy modeli predykcyjnych, który dla każdej obserwacji przypisuje wartość punktową dla wartości danej cechy. Metodą statystyczną wykorzystywaną w modelach skoringowych jest regresja logistyczna. Modele skoringowe są szczególnie popularne w bankach i innych instytucjach finansowych z uwagi na interpretowalność uzyskanych współczynników (uzyskane współczynniki można dość łatwo obliczyć ręcznie – regresja logistyczna jest metodą bardzo dobrze poznaną i opisaną). Popularnymi zastosowaniami modeli skoringowych jest obliczanie wartości „TAK lub „NIE” czyli wartości punktowych, że dana obserwacja należy do danej grupy.
W naszym przykładzie zbudujemy model skoringowy, w którym zmienną docelową będzie przynależność do grupy osób zdrowych. Wartości poszczególnych cech będą obniżać lub podwyższać wartość punktową w zakresie 0-100.
Import bibliotek:
import pandas as pd import numpy as np import seaborn as sns import matplotlib.pyplot as plt from sklearn.model_selection import train_test_split, RepeatedStratifiedKFold, cross_val_score from sklearn.linear_model import LogisticRegression from sklearn.metrics import roc_curve, roc_auc_score, confusion_matrix, precision_recall_curve, auc from sklearn.feature_selection import f_classif from sklearn.base import BaseEstimator, TransformerMixin from scipy.stats import chi2_contingency from sklearn.metrics import confusion_matrix from sklearn.metrics import accuracy_score
Import pliku:
loan_data = pd.read_csv(sciezkapliku.csv', encoding='latin-1', on_bad_lines='skip', sep=",")
Rzut oka na dane:
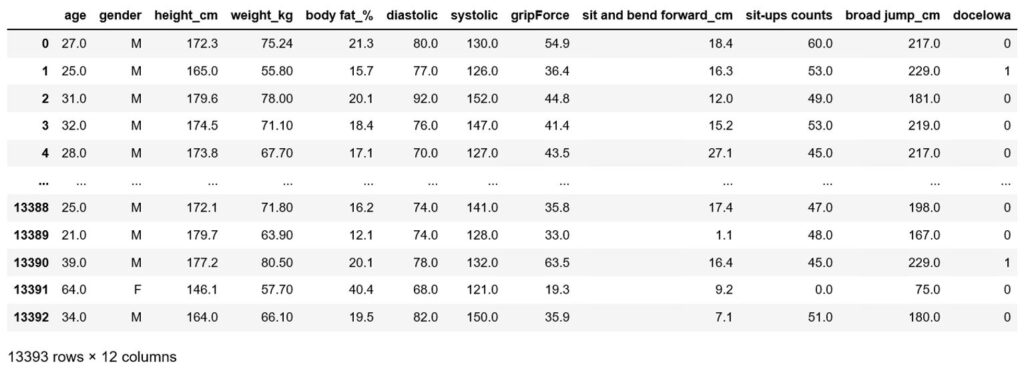
Dzielimy zbiór na treningowy i testowy:
X = loan_data.drop('docelowa', axis = 1)
y = loan_data['docelowa']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2,
random_state = 42, stratify = y)
Sprawdzamy rozkład zmiennej docelowej:
loan_data['docelowa'].value_counts()
sns.countplot(x='docelowa', data=loan_data, palette='hls')
plt.show()
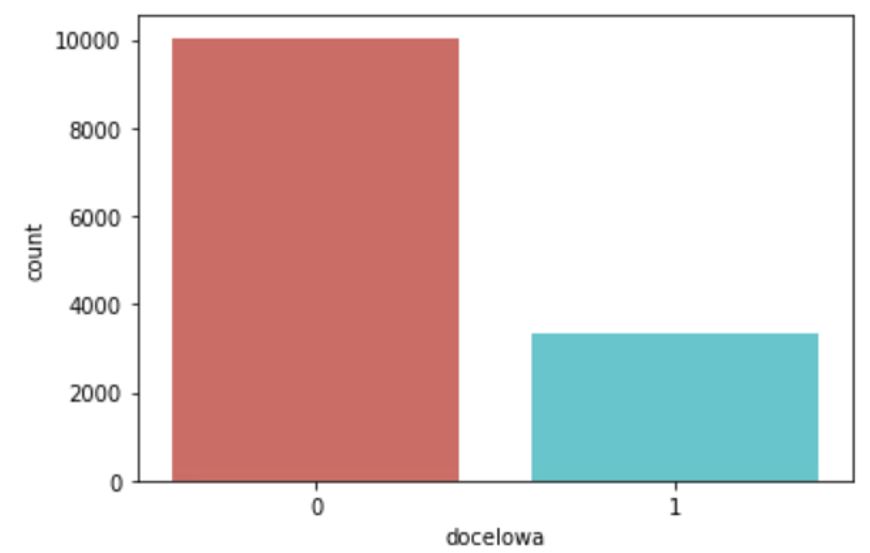
Zmienna zawiera więcej wartości negatywnych, zatem konieczne będzie zbalansowanie danych na późniejszym etapie modelowania.
W pierwszym etapie usuwamy zmienne objaśniające skorelowane – pozostawienie zmiennej nadmiernie skorelowanej nie wnosi nowych informacji do modelu oraz sztucznie zawyża współczynniki dla tej zmiennej oraz całkowitej skuteczności modelu.
Wyznaczamy macierz korelacji:
corr = loan_data.corr()
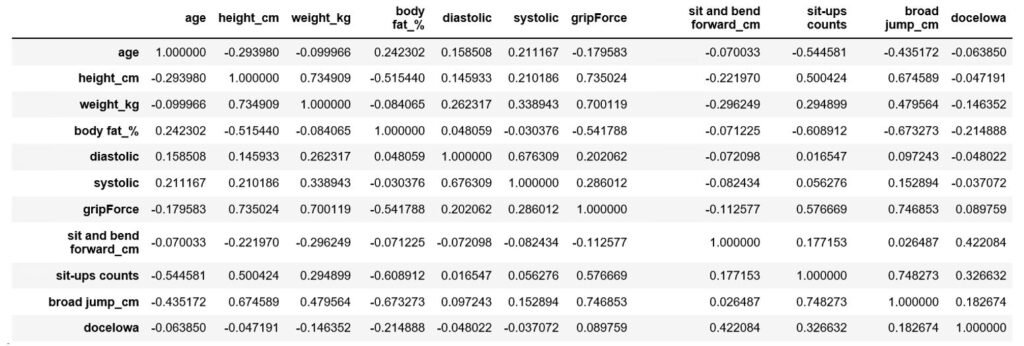
I wyznaczamy pary szczególnie skorelowane (w naszym przykładzie z korelacją > 50%)
high_corr_var=np.where(corr>0.5)
high_corr_var=[(corr.columns[x],corr.columns[y]) for x,y in zip(*high_corr_var) if x!=y and x<y]

Usuwamy po jednej zmiennej z każdej pary. Zostawiamy zmienną z większą korelacją ze zmienną docelową.
drop_columns_list = ['height_cm','systolic','gripForce','broad jump_cm']
def col_to_drop(df, columns_list):
df.drop(columns = columns_list, inplace = True)
col_to_drop(X_train, drop_columns_list) col_to_drop(X_test, drop_columns_list)
Kolejnym etapem jest wykluczenie zmiennych ”słabych”, które mają niski wpływ na rozróżnianie zmiennej docelowej. W przypadku modeli skoringowych, decydującym wskaźnikiem jest WoE (Weight of Evidence):
def woe_ordered_continuous(df, continuous_variabe_name, y_df):
df = pd.concat([df[continuous_variabe_name], y_df], axis = 1)
df = pd.concat([df.groupby(df.columns.values[0], as_index = False)[df.columns.values[1]].count(),
df.groupby(df.columns.values[0], as_index = False)[df.columns.values[1]].mean()], axis = 1)
df = df.iloc[:, [0, 1, 3]]
df.columns = [df.columns.values[0], 'n_obs', 'prop_good']
df['prop_n_obs'] = df['n_obs'] / df['n_obs'].sum()
df['n_good'] = df['prop_good'] * df['n_obs']
df['n_bad'] = (1 - df['prop_good']) * df['n_obs']
df['prop_n_good'] = df['n_good'] / df['n_good'].sum()
df['prop_n_bad'] = df['n_bad'] / df['n_bad'].sum()
df['WoE'] = np.log(df['prop_n_good'] / df['prop_n_bad'])
#df = df.sort_values(['WoE'])
#df = df.reset_index(drop = True)
df['diff_prop_good'] = df['prop_good'].diff().abs()
df['diff_WoE'] = df['WoE'].diff().abs()
df['IV'] = (df['prop_n_good'] - df['prop_n_bad']) * df['WoE']
df['IV'] = df['IV'].replace([np.inf, -np.inf], np.nan)
return df
lista=X_train.columns
lista2=[]
for element in lista:
df_WoE = woe_ordered_continuous(X_train, element, y_train)
dod=df_WoE['IV'].sum()
lista2.append(dod)
lista2, lista

Zmienne poniżej 0,05 przyjmuje się za szczególnie słabe, a powyżej 0,7 za nadmiernie wysokie, zatem z modelu usuwamy zmienne „gender”, „diastolic”, „sit and bend forward_cm”.
Usuwamy zatem te zmienne:
drop_columns_list=['gender','diastolic']
col_to_drop(X_train, drop_columns_list)
col_to_drop(X_test, drop_columns_list)
Następnym krokiem jest skategoryzowanie zmiennych. Algorytmy wyszukują optymalne punkty podziału zapewniające jak najskuteczniejsze rozróżnianie zmiennych z jak najmniejszą stratą informacji. Zaletą tego rozwiązania jest możliwość dokładnego modelowania informacji nieliniowych.
c = toad.transform.Combiner()
c.fit(X=X_train,y = y_train,method = 'chi',min_samples = 0.05,n_bins = None)
c.export()
Punkty podziału są następujące:

Wg wyznaczonych punktów należy teraz podzielić nasze zmienne. Istnieją algorytmy, które wykonują to automatycznie, ale chcąc mieć większą kontrolę wykonuję to ręcznie:
X_train['age_<=25'] = np.where(X_train['age'] <= 25, 1,0)
X_train['age_25_28'] = np.where((X_train['age'] <= 28) & (X_train['age'] > 25), 1,0)
X_train['age_28_31'] = np.where((X_train['age'] <= 31) & (X_train['age'] > 28), 1,0)
X_train['age_31_39'] = np.where((X_train['age'] <= 39) & (X_train['age'] > 31), 1,0)
X_train['age_39_52'] = np.where((X_train['age'] <= 52) & (X_train['age'] > 39), 1,0)
X_train['age_52_60'] = np.where((X_train['age'] <= 60) & (X_train['age'] > 52), 1,0)
X_train['age_>60'] = np.where(X_train['age'] > 60, 1,0)
X_train['weight_kg_<=52.2'] = np.where(X_train['weight_kg'] <= 52.2, 1,0)
X_train['weight_kg_52_58'] = np.where((X_train['weight_kg'] <= 58.4) & (X_train['weight_kg'] > 52.2), 1,0)
X_train['weight_kg_58_73'] = np.where((X_train['weight_kg'] <= 73) & (X_train['weight_kg'] > 58.4), 1,0)
X_train['weight_kg_73_78'] = np.where((X_train['weight_kg'] <= 78.6) & (X_train['weight_kg'] > 73), 1,0)
X_train['weight_kg_78_85'] = np.where((X_train['weight_kg'] <= 85.4) & (X_train['weight_kg'] > 78.6), 1,0)
X_train['weight_kg_>85'] = np.where(X_train['weight_kg'] > 85.4, 1,0)
X_train['body fat_%_<=16'] = np.where(X_train['body fat_%'] <= 16.1, 1,0)
X_train['body fat_%_16_19'] = np.where((X_train['body fat_%'] <= 19.8) & (X_train['body fat_%'] > 16.1), 1,0)
X_train['body fat_%_19_23'] = np.where((X_train['body fat_%'] <= 23.7) & (X_train['body fat_%'] > 19.8), 1,0)
X_train['body fat_%_23_28'] = np.where((X_train['body fat_%'] <= 28.4) & (X_train['body fat_%'] > 23.7), 1,0)
X_train['body fat_%_28_34'] = np.where((X_train['body fat_%'] <= 34.3) & (X_train['body fat_%'] > 28.4), 1,0)
X_train['body fat_%_>34'] = np.where(X_train['body fat_%'] > 34.3, 1,0)
X_train['sit-ups counts_<=17'] = np.where(X_train['sit-ups counts'] <= 17, 1,0)
X_train['sit-ups counts_17_31'] = np.where((X_train['sit-ups counts'] <= 31) & (X_train['sit-ups counts'] > 17), 1,0)
X_train['sit-ups counts_31_37'] = np.where((X_train['sit-ups counts'] <= 37) & (X_train['sit-ups counts'] > 31), 1,0)
X_train['sit-ups counts_37_47'] = np.where((X_train['sit-ups counts'] <= 47) & (X_train['sit-ups counts'] > 37), 1,0)
X_train['sit-ups counts_47_54'] = np.where((X_train['sit-ups counts'] <= 54) & (X_train['sit-ups counts'] > 47), 1,0)
X_train['sit-ups counts_54_59'] = np.where((X_train['sit-ups counts'] <= 59) & (X_train['sit-ups counts'] > 54), 1,0)
X_train['sit-ups counts_>59'] = np.where(X_train['sit-ups counts'] > 59, 1,0)
Procedurę powtarzam dla zbioru testowego:
X_test['age_<=25'] = np.where(X_test['age'] <= 25, 1,0)
X_test['age_25_28'] = np.where((X_test['age'] <= 28) & (X_test['age'] > 25), 1,0)
X_test['age_28_31'] = np.where((X_test['age'] <= 31) & (X_test['age'] > 28), 1,0)
X_test['age_31_39'] = np.where((X_test['age'] <= 39) & (X_test['age'] > 31), 1,0)
X_test['age_39_52'] = np.where((X_test['age'] <= 52) & (X_test['age'] > 39), 1,0)
X_test['age_52_60'] = np.where((X_test['age'] <= 60) & (X_test['age'] > 52), 1,0)
X_test['age_>60'] = np.where(X_test['age'] > 60, 1,0)
X_test['weight_kg_<=52.2'] = np.where(X_test['weight_kg'] <= 52.2, 1,0)
X_test['weight_kg_52_58'] = np.where((X_test['weight_kg'] <= 58.4) & (X_test['weight_kg'] > 52.2), 1,0)
X_test['weight_kg_58_73'] = np.where((X_test['weight_kg'] <= 73) & (X_test['weight_kg'] > 58.4), 1,0)
X_test['weight_kg_73_78'] = np.where((X_test['weight_kg'] <= 78.6) & (X_test['weight_kg'] > 73), 1,0)
X_test['weight_kg_78_85'] = np.where((X_test['weight_kg'] <= 85.4) & (X_test['weight_kg'] > 78.6), 1,0)
X_test['weight_kg_>85'] = np.where(X_test['weight_kg'] > 85.4, 1,0)
X_test['body fat_%_<=16'] = np.where(X_test['body fat_%'] <= 16.1, 1,0)
X_test['body fat_%_16_19'] = np.where((X_test['body fat_%'] <= 19.8) & (X_test['body fat_%'] > 16.1), 1,0)
X_test['body fat_%_19_23'] = np.where((X_test['body fat_%'] <= 23.7) & (X_test['body fat_%'] > 19.8), 1,0)
X_test['body fat_%_23_28'] = np.where((X_test['body fat_%'] <= 28.4) & (X_test['body fat_%'] > 23.7), 1,0)
X_test['body fat_%_28_34'] = np.where((X_test['body fat_%'] <= 34.3) & (X_test['body fat_%'] > 28.4), 1,0)
X_test['body fat_%_>34'] = np.where(X_test['body fat_%'] > 34.3, 1,0)
X_test['sit-ups counts_<=17'] = np.where(X_test['sit-ups counts'] <= 17, 1,0)
X_test['sit-ups counts_17_31'] = np.where((X_test['sit-ups counts'] <= 31) & (X_test['sit-ups counts'] > 17), 1,0)
X_test['sit-ups counts_31_37'] = np.where((X_test['sit-ups counts'] <= 37) & (X_test['sit-ups counts'] > 31), 1,0)
X_test['sit-ups counts_37_47'] = np.where((X_test['sit-ups counts'] <= 47) & (X_test['sit-ups counts'] > 37), 1,0)
X_test['sit-ups counts_47_54'] = np.where((X_test['sit-ups counts'] <= 54) & (X_test['sit-ups counts'] > 47), 1,0)
X_test['sit-ups counts_54_59'] = np.where((X_test['sit-ups counts'] <= 59) & (X_test['sit-ups counts'] > 54), 1,0)
X_test['sit-ups counts_>59'] = np.where(X_test['sit-ups counts'] > 59, 1,0)
I usuwam zmienne ciągłe:
drop_columns_list=['sit-ups counts','body fat_%','age','weight_kg']
col_to_drop(X_train, drop_columns_list)
col_to_drop(X_test, drop_columns_list)
Dane są gotowe do modelowania. Skuteczność na zbiorze testowym wyznaczam za pomocą walidacji krzyżowej:
reg = LogisticRegression(max_iter=1000, class_weight = 'balanced')
cv = RepeatedStratifiedKFold(n_splits=5, n_repeats=3, random_state=1)
scores = cross_val_score(reg, X_train, y_train, scoring = 'roc_auc', cv = cv)
AUROC = np.mean(scores)
GINI = AUROC * 2 - 1
print('Mean AUROC: %.4f' % (AUROC))
print('Gini: %.4f' % (GINI))

AUROC na poziomie 0,81 to dobry wynik. W związku z tym, ze zmienna docelowa jest niezbalansowana, użyłem metody class_weight „balanced”, która „karze” obserwacje występujące częściej, nadając im mniejsze współczynniki
Przystępuję zatem do treningu klasyfikatora:
reg.fit(X_train, y_train)
I obliczania skuteczności na zbiorze testowym:
y_hat_test = reg.predict(X_test)
y_hat_test_proba = reg.predict_proba(X_test)
y_hat_test_proba = y_hat_test_proba[:][: , 1]
y_test_temp = y_test.copy()
y_test_temp.reset_index(drop = True, inplace = True)
y_test_proba = pd.concat([y_test_temp, pd.DataFrame(y_hat_test_proba)], axis = 1)
y_test_proba.columns = ['y_test_class_actual', 'y_hat_test_proba']
y_test_proba.index = X_test.index
AUROC = roc_auc_score(y_test_proba['y_test_class_actual'], y_test_proba['y_hat_test_proba'])
Gini = AUROC * 2 - 1
cm = confusion_matrix(target, Y_pred_test)
print(f'Accuracy: {accuracy_score(target, Y_pred_test)}')
print('AUROC: %.4f' % (AUROC))
print('Gini: %.4f' % (Gini))

Wyznaczam także dodatkowe metryki skuteczności: macierz błędów oraz ogólną skuteczność klasyfikacji:
color = 'black'
matrix = plot_confusion_matrix(reg, X_test, y_test, cmap=plt.cm.Blues)
matrix.ax_.set_title('Confusion Matrix', color=color)
plt.xlabel('Predicted Label', color=color)
plt.ylabel('True Label', color=color)
plt.gcf().axes[0].tick_params(colors=color)
plt.gcf().axes[1].tick_params(colors=color)
Y_pred_test = reg.predict(X_test)
print(f'Accuracy: {accuracy_score(y_test, Y_pred_test)}')
plt.show()
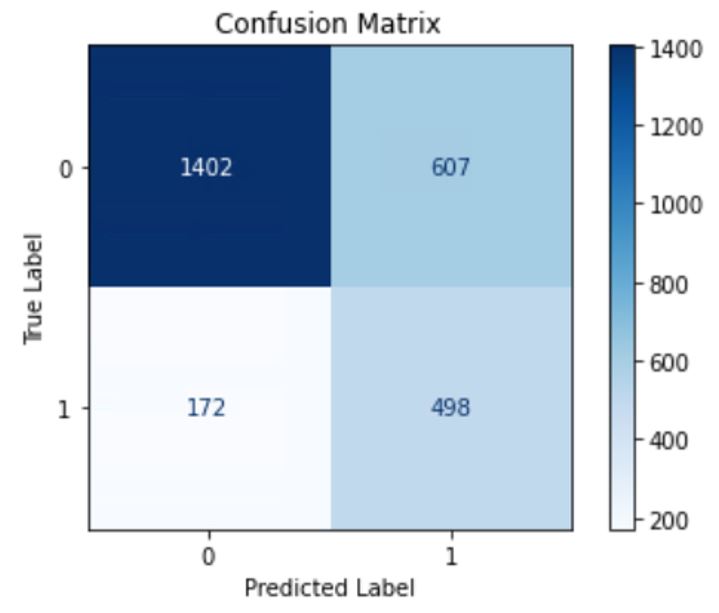
Skuteczność klasyfikacji na zbiorze testowym wyniosła 71%. Jest to akceptowalny wynik. Niepożądanym zjawiskiem jest skłonność modelu do traktowania obserwacji pozytywnych jako negatywnych. Przyczyną może być niezbalansowanie zmiennej docelowej.
Po wytrenowaniu modelu tworzymy ostateczną wersję karty.
feature_name = X_train.columns.values
summary_table = pd.DataFrame(columns = ['Feature name'], data = feature_name)
summary_table['Coefficients'] = np.transpose(reg.coef_)
summary_table.index = summary_table.index + 1
summary_table.loc[0] = ['Intercept', reg.intercept_[0]]
summary_table.sort_index(inplace = True)
ref_categories=X_train.columns
min_score = 0
max_score = 100
df_ref_categories = pd.DataFrame(ref_categories, columns = ['Feature name'])
df_ref_categories['Coefficients'] = 0
df_scorecard = pd.concat([summary_table, df_ref_categories])
df_scorecard.reset_index(inplace = True)
df_scorecard['Original feature name'] = df_scorecard['Feature name'].str.split(':').str[0]
min_sum_coef = df_scorecard.groupby('Original feature name')['Coefficients'].min().sum()
max_sum_coef = df_scorecard.groupby('Original feature name')['Coefficients'].max().sum()
df_scorecard['Score - Calculation'] = df_scorecard['Coefficients'] * (max_score - min_score) / (max_sum_coef - min_sum_coef)
df_scorecard.loc[0, 'Score - Calculation'] = (
(df_scorecard.loc[0,'Coefficients'] - min_sum_coef) /
(max_sum_coef - min_sum_coef)) * (max_score - min_score) + min_score
df_scorecard['Score - value'] = df_scorecard['Score - Calculation'].round()
Ostateczny rezultat:
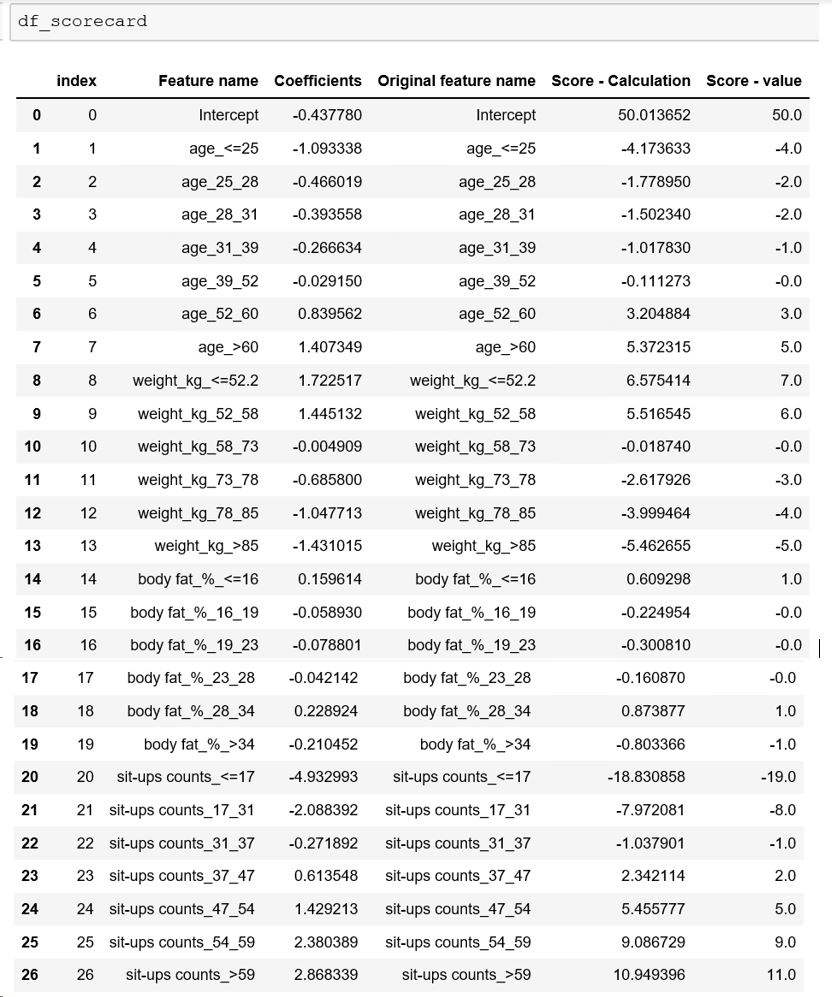
Dla każdej zmiennej mamy obliczoną wartość punktową. Punkty układają się w dużej mierze liniowo I tak, np. osoba, która wykona powyżej 59 przysiadów ma większe prawdopodobieństwo przynależenia do kategorii zdrowej i otrzyma aż +19 punktów.
Najzdrowsza osoba wg modelu, to ta która ma powyżej 60 lat, poniżej 52 kg, z poziomem tkanki tłuszczowej poniżej 16% i która wykonuje więcej niż 59 przysiadów 😊
Aby model wprowadzić „na produkcję”, wystarczy dla nowych obserwacji wyznaczyć do których kategorii dla tych czterech zmiennych należą i zsumować punkty.